Page 75 - Year 11 Knowledge Organiser

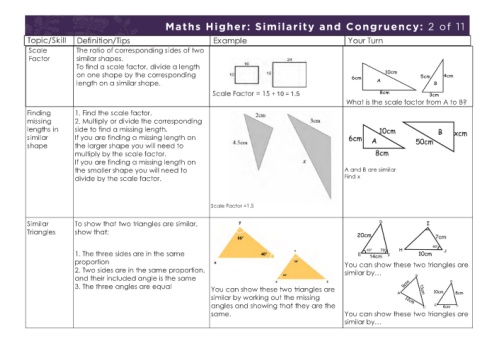
Maths Higher: Similarity and Congruency: 1 of 11 Maths Higher: Similarity and Congruency: 2 of 11

Topic/Skill Definition/Tips Example Your Turn Topic/Skill Definition/Tips Example Your Turn
Scale The ratio of corresponding sides of two
Congruent Shapes are congruent if they are Factor similar shapes.
Shape identical - same shape and same To find a scale factor, divide a length
size. on one shape by the corresponding
length on a similar shape.

Shapes can be rotated or reflected Scale Factor = 15 ÷ 10 = 1.5
but still be congruent. What is the scale factor from A to B?
Finding 1. Find the scale factor.
Congruent 4 ways of proving that two triangles missing 2. Multiply or divide the corresponding
Triangles are congruent: lengths in side to find a missing length.
similar If you are finding a missing length on
shapes the larger shape you will need to
1. SSS (Side, Side, Side) multiply by the scale factor.
2. RHS (Right angle, Hypotenuse, If you are finding a missing length on
Side) the smaller shape you will need to A and B are similar
3. SAS (Side, Angle, Side) divide by the scale factor. Find x
4. ASA (Angle, Side, Angle) or AAS

ASS does not prove congruency. Scale Factor =1.5

Similar To show that two triangles are similar,
Similar Shapes Shapes are similar if they are the Triangles show that:
same shape but different sizes.

1. The three sides are in the same
The proportion of the matching sides proportion
must be the same, meaning the 2. Two sides are in the same proportion, You can show these two triangles are
similar by…
ratios of corresponding sides are all and their included angle is the same
equal. 3. The three angles are equal You can show these two triangles are
similar by working out the missing
angles and showing that they are the
same. You can show these two triangles are
similar by…