Page 59 - Year 10 Knowledge Organiser

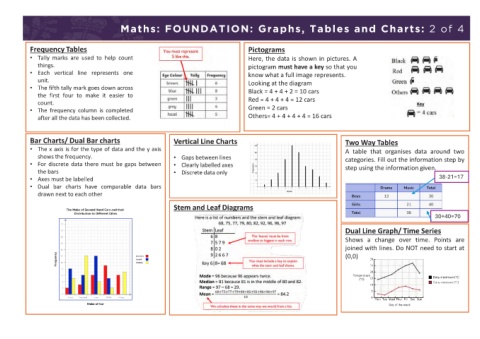
Maths: FOUNDATION: : Algebra: 1 of 4 Maths: FOUNDATION: Graphs, Tables and Charts: 2 of 4

Simplifying expressions Substitution Expressions as functions Frequency Tables Pictograms
You can simplify by: To substitute means to replace a letter for a • Tally marks are used to help count Here, the data is shown in pictures. A
Collecting like terms: Like terms are those with number. Expressions can be written as simple function things. pictogram must have a key so that you
the same letter and power. machines. • Each vertical line represents one know what a full image represents.
unit. Looking at the diagram
4b = 4 x 3 = 12 E.g. • The fifth tally mark goes down across Black = 4 + 4 + 2 = 10 cars
the first four to make it easier to
count. Red = 4 + 4 + 4 = 12 cars
7b – 3c = (7 x 3) – (3 x (-5)) = 21-(-15)= 36 3n+4 means multiply n by 3 then add 4 • The frequency column is completed Green = 2 cars
after all the data has been collected. Others= 4 + 4 + 4 + 4 = 16 cars

If the input was 2, the output would be Bar Charts/ Dual Bar charts Vertical Line Charts Two Way Tables
Using laws of indices Expanding brackets (3 x 2) + 4 = 10 • The x axis is for the type of data and the y axis A table that organises data around two
Start by writing out in full: shows the frequency. • Gaps between lines categories. Fill out the information step by
3 4 Multiply the term outside the bracket with each If the output was 25, we would be able to use • For discrete data there must be gaps between
= × × = × × × term inside the bracket. • Clearly labelled axes step using the information given.
3 4 7 inverse functions to work out what the input the bars • Discrete data only
So × = × × × × × × = 38-21=17
To multiply two terms with the same base you would have been. • Axes must be labelled
can add the powers. • Dual bar charts have comparable data bars
drawn next to each other
5
× × × × 2 Stem and Leaf Diagrams
= =
3 × × 30+40=70
To divide two terms with the same base you can
subtract the powers. Factorising Using algebra to solve problems Dual Line Graph/ Time Series
Shows a change over time. Points are
If you need to multiply a combination of To factorise means to put into brackets. We can use expressions to work out joined with lines. Do NOT need to start at
numbers and powers, work with the numbers different values for real life problems. (0,0)
separately first: Find the highest common factor for both terms E.g.
(this might be a letter or a number or both) The amount of medicine (m) in ml needed is two

× = × × × = times the weight in kg, divided by 10. Work out
the amount of medicine for a 15kg child.
4
4 2
4
( ) × = 8 m= 2
If you have a power raised to a power, you can 2×15
10
multiply the powers so for this child m = 10 = 30 ÷ 10 = 3 .